Árbol (Tree)
En esta Página
Un árbol es una estructura de datos que simula una estructura de árbol jerárquica, con un valor raíz y subárboles de hijos con un nodo padre.
Se define de forma recursiva como una colección de nodos, empezando por un nodo raíz, donde cada nodo es una estructura de datos que contiene un valor, y opcionalmente una lista de referencias a otros nodos (sus hijos), con la limitación de que ninguna referencia esté duplicada, y que ninguna apunte al nodo raíz.
Los árboles se utilizan en diversos contextos, como por ejemplo:
- En la representación de jerarquías.
- En la estructura del DOM (Document Object Model) en desarrollo web.
- En algoritmos de aprendizaje supervisado no paramétrico, como los árboles de decisión.
- En la representación de grafos acíclicos dirigidos y mínimamente conectados.
Binary Tree (Árbol Binario)
Un árbol binario es una estructura de datos en forma de árbol en la que cada nodo puede tener como máximo dos hijos, conocidos como el hijo izquierdo y el hijo derecho.
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor() {
this.root = null;
}
// Agrega un nodo al árbol binario
add(data) {
const newNode = new Node(data);
if (this.root === null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
}
// Inserta un nodo en el árbol binario
insertNode(node, newNode) {
if (newNode.data < node.data) {
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
}
// Recorre el árbol binario en orden
inorder(node) {
if (node !== null) {
this.inorder(node.left);
console.log(node.data);
this.inorder(node.right);
}
}
}
// Usando el árbol binario
const BT = new BinaryTree();
BT.add(15);
BT.add(25);
BT.add(10);
BT.add(7);
BT.add(22);
BT.add(17);
BT.add(13);
BT.add(5);
BT.add(9);
BT.add(27);
BT.inorder(BT.root); // imprime los nodos en ordenEn este código, la clase Node representa un nodo en el árbol binario. Cada nodo tiene un data que almacena el valor del nodo, un left que es el nodo hijo izquierdo y un right que es el nodo hijo derecho.
La clase BinaryTree representa el árbol binario. Tiene un root que es el nodo raíz del árbol. También tiene métodos para agregar un nodo al árbol (add), insertar un nodo en el árbol (insertNode), y recorrer el árbol en orden (inorder).
Eliminar un nodo en un árbol binario de búsqueda en JavaScript puede ser un poco complicado porque hay varias situaciones que debes considerar:
- El nodo a eliminar es una hoja (no tiene hijos).
- El nodo a eliminar tiene un solo hijo.
- El nodo a eliminar tiene dos hijos.
Aquí te muestro cómo puedes hacerlo:
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor() {
this.root = null;
}
// ... otros métodos ...
// Elimina un nodo del árbol binario
remove(data) {
this.root = this.removeNode(this.root, data);
}
// Elimina un nodo del árbol binario
removeNode(node, key) {
if (node === null) {
return null;
} else if (key < node.data) {
node.left = this.removeNode(node.left, key);
return node;
} else if (key > node.data) {
node.right = this.removeNode(node.right, key);
return node;
} else {
if (node.left === null && node.right === null) {
node = null;
return node;
}
if (node.left === null) {
node = node.right;
return node;
} else if (node.right === null) {
node = node.left;
return node;
}
let aux = this.findMinNode(node.right);
node.data = aux.data;
node.right = this.removeNode(node.right, aux.data);
return node;
}
}
// Encuentra el nodo con el valor mínimo
findMinNode(node) {
if (node.left === null)
return node;
else
return this.findMinNode(node.left);
}
}
// Usando el árbol binario
const BT = new BinaryTree();
BT.add(15);
BT.add(25);
BT.add(10);
BT.add(7);
BT.add(22);
BT.add(17);
BT.add(13);
BT.add(5);
BT.add(9);
BT.add(27);
BT.remove(5);
BT.inorder(BT.root); // imprime los nodos en ordenEn este código, la clase BinaryTree tiene un método remove que elimina un nodo del árbol. Este método llama a removeNode, que es un método recursivo que busca el nodo a eliminar y lo elimina de acuerdo a las reglas mencionadas anteriormente. Si el nodo a eliminar tiene dos hijos, se busca el nodo con el valor mínimo en el subárbol derecho (usando findMinNode), se copia su valor al nodo a eliminar y luego se elimina el nodo con el valor mínimo.
Binary Search Tree (Árbol de búsqueda binaria)
Un árbol de búsqueda binaria, también llamado árbol binario ordenado o clasificado, es una estructura de datos de árbol binario con raíz, donde la clave de cada nodo interno es mayor que todas las claves en el subárbol izquierdo respectivo y menor que las claves en el subárbol derecho.
Full Binary Tree (Árbol binario propio)
Un árbol binario propio es un tipo especial de árbol binario en el que cada nodo padre o nodo interno tiene ya sea dos o ningún hijo. También se conoce como un árbol binario propio.
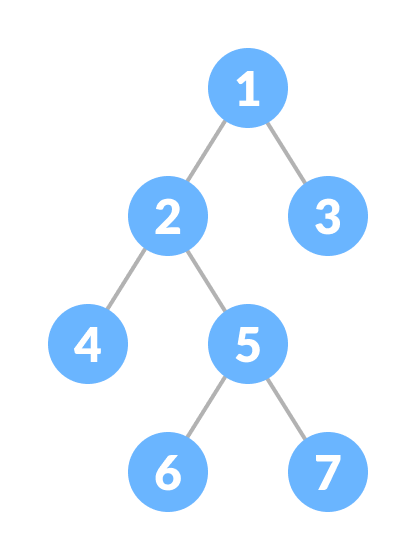
Complete Binary Tree (Árbol binario completo)
Un árbol binario completo es un árbol binario en el que todos los niveles están completamente llenos, excepto posiblemente el más bajo, que se llena desde la izquierda.
Un árbol binario completo es similar a un árbol binario propio, pero con dos diferencias importantes:
- Todos los elementos hoja deben inclinarse hacia la izquierda.
- El último elemento hoja puede no tener un hermano derecho, es decir, un árbol binario completo no tiene que ser un árbol binario propio.
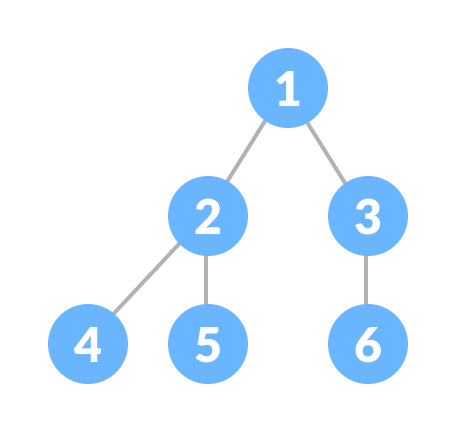
Balanced Tree (Árbol binario equilibrado)
Un árbol binario equilibrado, también conocido como árbol binario balanceado en altura, se define como un árbol binario en el que la diferencia de altura entre el subárbol izquierdo y el subárbol derecho de cualquier nodo no es mayor que 1.
Aquí te muestro cómo puedes implementar un árbol AVL en JavaScript:
class Node {
constructor(data, left = null, right = null) {
this.data = data;
this.left = left;
this.right = right;
this.height = 1;
}
}
class AVLTree {
constructor() {
this.root = null;
}
getHeight(node) {
if (node === null) {
return 0;
}
return node.height;
}
getBalance(node) {
if (node === null) {
return 0;
}
return this.getHeight(node.left) - this.getHeight(node.right);
}
leftRotate(node) {
let rightNode = node.right;
let rightLeftNode = rightNode.left;
rightNode.left = node;
node.right = rightLeftNode;
node.height = Math.max(this.getHeight(node.left), this.getHeight(node.right)) + 1;
rightNode.height = Math.max(this.getHeight(rightNode.left), this.getHeight(rightNode.right)) + 1;
return rightNode;
}
rightRotate(node) {
let leftNode = node.left;
let leftRightNode = leftNode.right;
leftNode.right = node;
node.left = leftRightNode;
node.height = Math.max(this.getHeight(node.left), this.getHeight(node.right)) + 1;
leftNode.height = Math.max(this.getHeight(leftNode.left), this.getHeight(leftNode.right)) + 1;
return leftNode;
}
insert(data) {
this.root = this.insertNode(this.root, data);
}
insertNode(node, data) {
if (node === null) {
return new Node(data);
} else if (data < node.data) {
node.left = this.insertNode(node.left, data);
} else if (data > node.data) {
node.right = this.insertNode(node.right, data);
} else {
return node;
}
node.height = 1 + Math.max(this.getHeight(node.left), this.getHeight(node.right));
let balance = this.getBalance(node);
if (balance > 1 && data < node.left.data) {
return this.rightRotate(node);
}
if (balance < -1 && data > node.right.data) {
return this.leftRotate(node);
}
if (balance > 1 && data > node.left.data) {
node.left = this.leftRotate(node.left);
return this.rightRotate(node);
}
if (balance < -1 && data < node.right.data) {
node.right = this.rightRotate(node.right);
return this.leftRotate(node);
}
return node;
}
}
// Usando el árbol AVL
let avlTree = new AVLTree();
avlTree.insert(10);
avlTree.insert(20);
avlTree.insert(30);
avlTree.insert(40);
avlTree.insert(50);
avlTree.insert(25);En este código, la clase Node representa un nodo en el árbol AVL. Cada nodo tiene un data que almacena el valor del nodo, un left que es el nodo hijo izquierdo, un right que es el nodo hijo derecho, y una height que es la altura del nodo.
La clase AVLTree representa el árbol AVL. Tiene un root que es el nodo raíz del árbol. También tiene métodos para obtener la altura de un nodo (getHeight), obtener el factor de equilibrio de un nodo (getBalance), rotar un nodo a la izquierda (leftRotate), rotar un nodo a la derecha (rightRotate), e insertar un nodo en el árbol (insert). El método insert llama a insertNode, que es un método recursivo que inserta un nodo en el árbol y luego equilibra el árbol.
Unbalanced Tree (Árbol binario desequilibrado)
Un árbol binario desequilibrado es aquel que no cumple con las condiciones de equilibrio, es decir, la diferencia de altura entre el subárbol izquierdo y el subárbol derecho de al menos un nodo es mayor que 1. Esto puede resultar en un rendimiento subóptimo en términos de tiempo de búsqueda y otras operaciones en comparación con árboles balanceados.